旋转设计rotation design

具有旋转性统计性质的回归设计。在编码值因子空间内与中心点等距的同一球面上各点的预测值方差都相等称为旋转性。旋转性减少了回归方程寻优的误差干扰，是一项重要的统计性质。二次正交回归设计不具有旋转性，预测值间的互比较为困难，旋转设计改善了这些不足。p元d次旋转设计的信息矩阵A是C^d_p+d阶对称方阵。A中

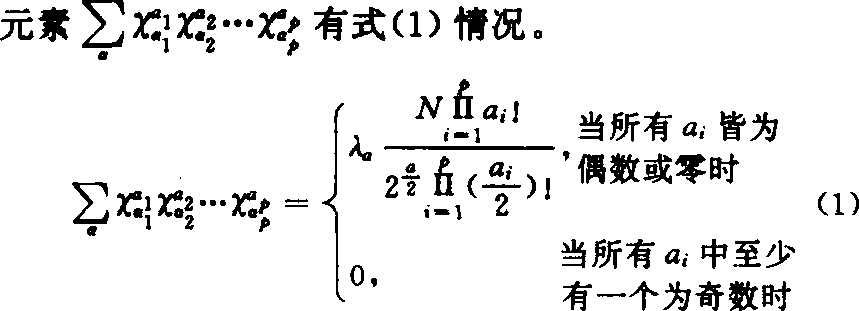
式(1)中 指数a为各试验因素的次数，a₁、a₂、…a_p为非负整数，N为试验方案的处理组合数，λ_a为待定参数，其下标为偶数，但λ0=1，式(1)称为旋转性条件。
应用最广的是p元二次旋转设计，其回归模型为：

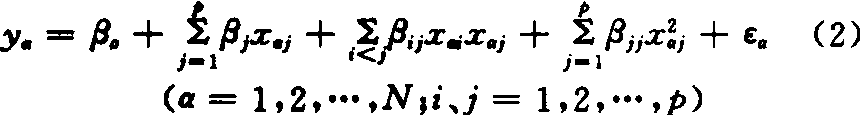
旋转设计也是组合设计，N个处理分为三个部分：
N=m_c+2p+m₀ (3)
它们分布在三个半径ρ不等的球面上：m_c个点在半径ρ_c为的球面上；2p个点分布在半径ρ_r为γ的球面上；m₀个点在球心上，即ρ₀＝0。对不同因素数p的旋转设计，于区间0<ρ<1内，预测值方差基本不变的性质称为通用性。具备通用性的旋转设计使编码值-1至1的因子空间内预测方差基本相等，寻优时可使各个预测值y直接互比，这是十分重要的统计性质。满足旋转性与通用性要求的试验称为通用旋转设计，模型(2)的通用旋转设计的参数表(表1):

表1 二次通用旋转设计的参数表

因素数P	mc	Zp	m0	N	γ
2 3 4 5 5(1/2实施) 6(1/2实施)	4 8 16 32 16 32	4 6 8 10 10 12	5 6 7 10 6 9	13 20 31 52 32 53	1.414 1.682 2.000 2.378 2.000 2.378

按照二次通用旋转设计的设计参数进行试验设计，各因素不同的编码水平亦为γ、1、0、-1、-γ。由于采用通用性导致常数项及二次项丧失正交性，回归系数的计算方法略有不同，可按式(3)计算。

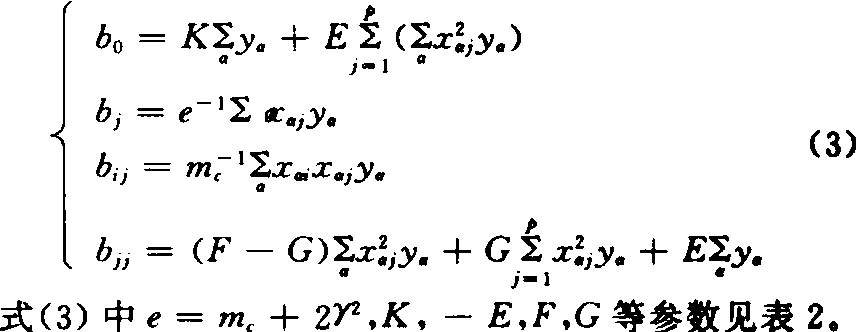
表2 二次通用旋转设计计算回归系数的参数

因素数P	K	-E	F	G
2 3 4 5 5(1/2实施) 6(1/2实施)	0.2 0.1663402 0.1428571 0.0987822 0.1590909 0.1107487	0.1 0.056792 0.0357142 0.19101 0.0340909 0.018738	0.14375 0.06939 0.0349702 0.170863 0.0340909 0.0168422	0.01875 0.00689003 0.00372023 0.00146131 0.0028409 0.00121724

进一步按部分处理有重复的回归方程的方法进行显著性检验（见线性回归），最后进行寻优，这时在因子空间编码值-1至1之间的预测值因误差方差几乎相等而可直接比较。由于二次通用旋转设计具有如上优点，受到农化工作者的重视，在多因素肥料中应用十分广泛。