复数的减法fushu de jianfa
加法的逆运算,即把满足
(c+di)+(x+yi)=a+bi
的复数x+yi叫做复数a+bi减去复数c+di所得的差.记作(a+bi)-(c+di).由复数相等的意义易得出x=a-c,y=b-d.于是有(a+bi)-(c+di)=(a-c)+(b-d)i
因为-c-di是c+di的相反复数,而(a+bi)+(-c-di)=(a-c)+(b-d)i=(a+bi)-(c+di).所以复数减法法则是:减去某复数等于加上它的相反复数.显然两个复数的差仍是一个复数.若复数z=a+bi对应的向量是
 ,z1=c+di对应的向量是
,z1=c+di对应的向量是 容易证明复数z=a+bi减去复数z1=c+di所得的差z2=(a-c)+(b-d)i所对应的向量就是
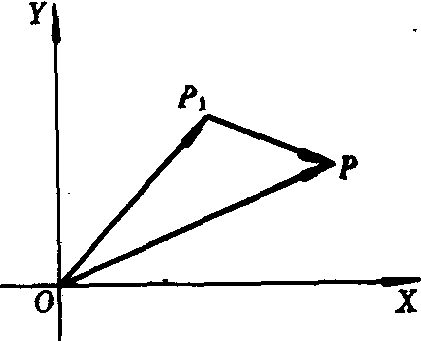
容易证明复数z=a+bi减去复数z1=c+di所得的差z2=(a-c)+(b-d)i所对应的向量就是 (如图),即连结两个向量终点并指向被减数的向量.这也是复数减法的几何解释(几何意义)及用求向量差的三角形法则来进行两个复数相减的几何方法.
(如图),即连结两个向量终点并指向被减数的向量.这也是复数减法的几何解释(几何意义)及用求向量差的三角形法则来进行两个复数相减的几何方法.